September 6, 2023

Derivation of Physically Based Rendering

The physical model and mathematical justification for physically based rendering.

Physically based rendering (PBR) is a general term for techniques in 3D graphics that approximate physical laws. The term PBR has come to generally mean techniques which aim for realistic rendering of real world materials. The PBR approach developed by Disney in 2012 still forms the basis of real-time rendering of realistic materials. This post explains the physical models and mathematics behind PBR. Hopefully by the end you will have justified why PBR shaders, for example this GLSL shader, look physically correct.

A dielectric (not metallic) material lit by a directional light following a PBR model.

Principles

To realistically render materials in a consistent manner some important laws should be obeyed.

Conservation of energy, the energy of light hitting a surface is less than or equal to the energy reflected.
Law of reflection, the incident angle equals the reflected angle for light reflecting off a mirror.
Fresnel Equations, the proportion of light reflected or transmitted when hitting a surface follows the Fresnel equations.

Accurately simulating all the behaviors of light is infeasible for real-time graphics, various simplifying assumptions about light are made in PBR including:

Light is always unpolarized.
Light's wave properties can be ignored (eg. diffraction, interference) and treated as rays, this is called geometry optics.
Light acts the same going from a light source to viewer as vice versa, called Helmholtz reciprocity.

These assumptions rarely cause problems which are visible, but certain situations or materials can exaggerate errors. For example, when multiple reflections occur between metallic surfaces, accounting for polarization can visibly change the result.

The Model

For each pixel on the screen imagine a ray which travels from a virtual eye and through the pixel's location on the image plane. The ray will eventually hit an object. If the object is opaque (ignoring atmospheric effects) the colour of that pixel will be determined by the light the object scatters from that point towards the pixel. PBR is about calculating the intensity of this scattered light.

Illustration of our physical model.

Radiance and Irradiance

Intensity is an general term, radiance and irradiance are two more specific physical units of light intensity. Radiance and irradiance technically have the same physical units of watts per square metre () but understanding the difference between the two is key to ensuring PBR conserves energy.

Irradiance

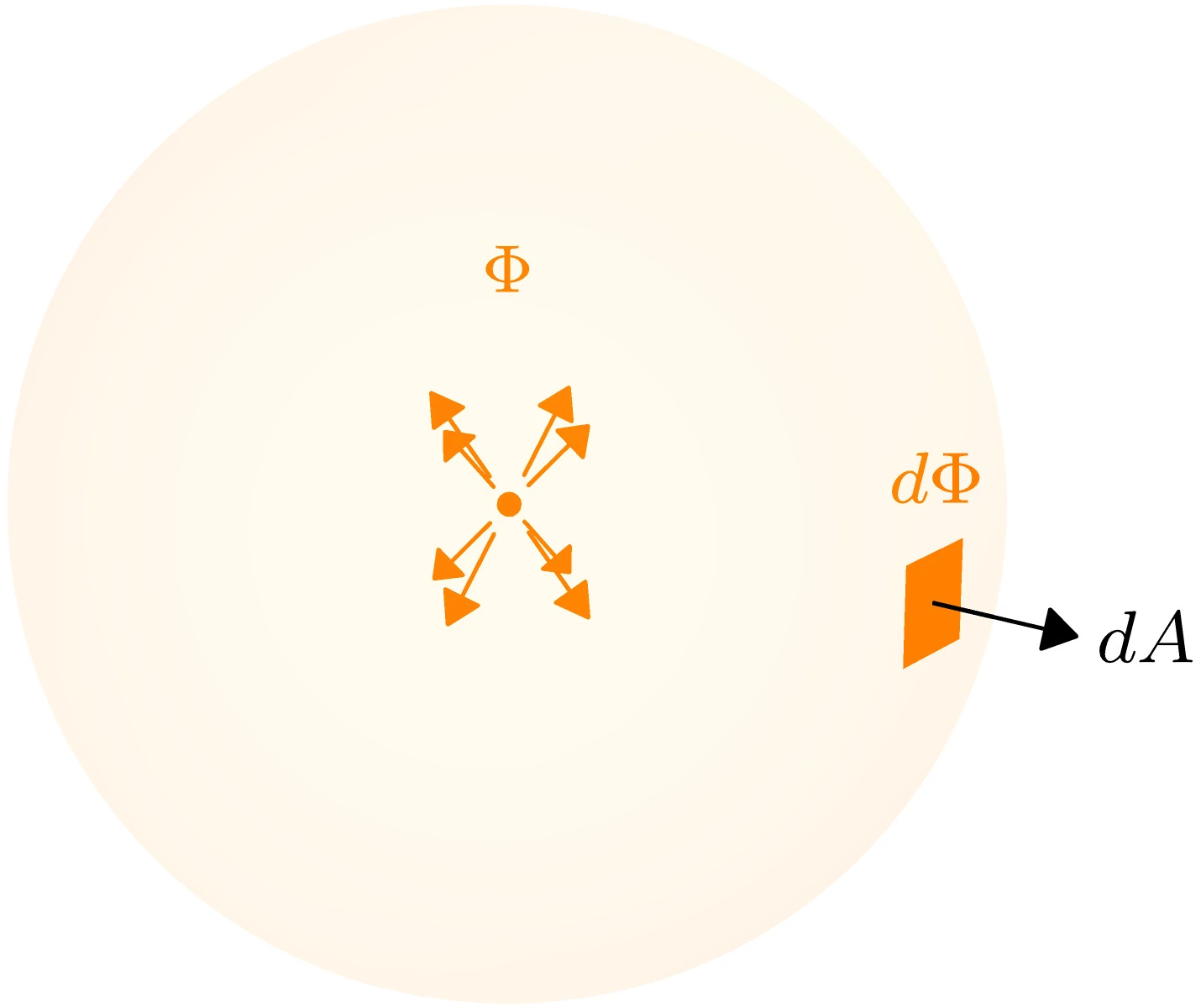
Irradiance is the relative flux through or onto an area.

Imagine a point emitting light in every direction with a total radiant flux of watts (joules per second). If we stand farther away from the light source, the flux is spread over a larger area. Imagine an area , in this case it happens to lie on the sphere's surface but it could be anywhere. Some amount of flux from the light source passes through this area. If we moved the area farther from the light source, the area appears "dim". If we increased the area and captured more flux, the area would still be "dim". The intensity we care about is then the amount of flux relative to the area it passes through. The irradiance is then

The notation indicates that the area is very small, this will be useful because it means the area is flat and has a normal.

Radiance

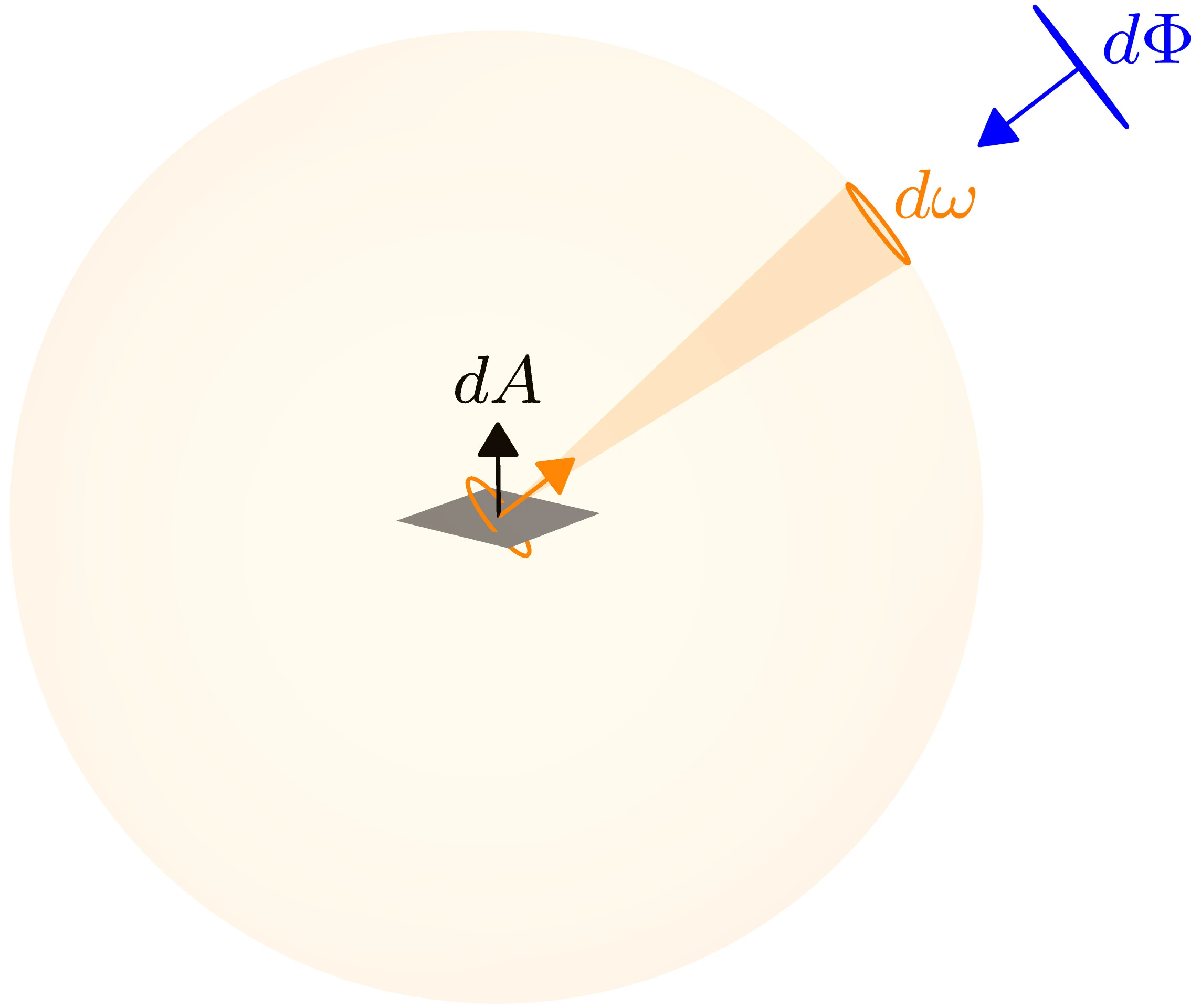
Radiance is the flux from a certain direction onto or reflected from an area.

Irradiance considers flux coming from every direction, but in rendering we want to know the light from a certain direction. Radiance is the directional form of irradiance. Unfortunately, if we looked at the flux from exactly one direction it would always be zero. To resolve this, imagine a unit sphere surrounding our area, we consider all flux which enters through a small "patch" on the surface. The location of the patch corresponds to the direction of our radiance and since our patch has a surface area, the flux can be non-zero.

This patch is analogous to the arc of a circle. The length of an arc is measured in radians, the patch's area is measured in steradians.

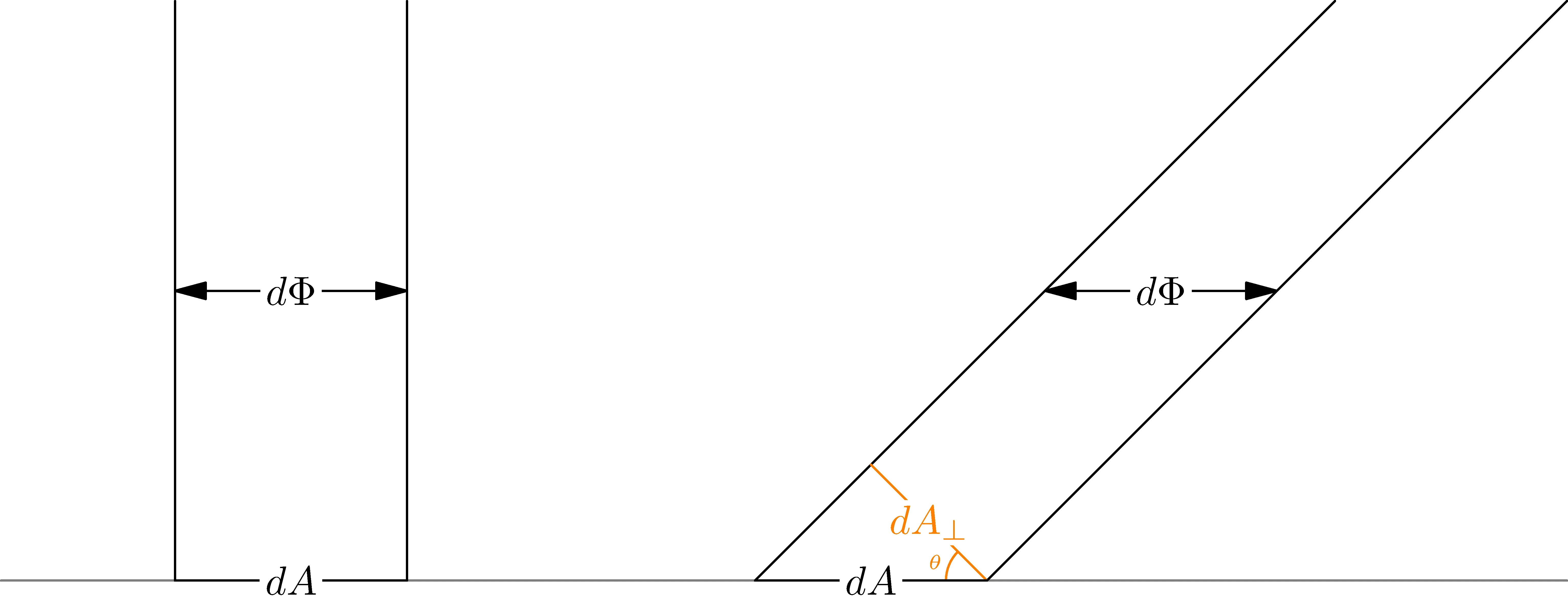
Projecting the area so it is perpendicular to the flux.

If the area is not perpendicular to the direction the flux is coming from, the flux through the area is not the same as the flux as if was oriented towards . This is demonstrated visually in the diagram. To ensure the orientation of the surface doesn't affect the radiance, is projected towards the radiance direction. Our projected area is where is the angle between the area's normal and direction of the radiance.

Putting together our projected area and the solid angle with the definition of steradians, radiance from a direction is

To further explain this definition, just as an arc length is equal to , the surface area of our patch is the projected area multiplied by . As with irradiance, we divide flux by the area it passes through and since we are only considering flux entering out patch, we need to divide the incoming flux by the patch area. The notation again indicates a small quantity, in practice the area can be treated as a point (eg. ) and the solid angle a ray.

The reason why radiance is defined for a patch on a sphere is that it makes the radiance of a light source independent of the distance and intrinsic to the light source. This can be illustrating by considering the following, as the distance from a light source increases, the flux into our patch decreases following the inverse square law , but the total solid angle occupied by the light source also decreases , cancelling out.

We can find irradiance onto an area by adding radiances from all incident directions, which define as here,

where projects the flux from back onto the irradiance area . I have also given the conversion in polar form, using , since this will be used later.

Formally, radiance is the radiant flux () per unit solid angle () in the direction of a ray per unit projected area () perpendicular to the ray.

In this post we are going to assume that the radiance of each light in a scene is known and take up an infinitesimal solid angle. This models directional lights such as the sun.

Colour

Spectral power distribution of sunlight.

The radiances we deal with will vary with the wavelength (i.e. colour) of the light. We could calculate the radiance for every visible wavelength, called a spectral power distribution (SPD), but this would be very computationally expensive. Luckily, we can approximate the perceived SPD by combining red, green and blue (RGB) radiances. For this reason, consider radiance, and any other spectral quantities, as RGB vectors.

Rendering Equation

If we consider our physical model again, we only care about flux directed towards the pixel from the object. Light from other directions is not focused by a camera's lens or the cornea. The pixel's colour is determined by the radiance scattered towards the pixel from the intersection point with the object's surface.

The light the object scatters towards our eye is either reflected from the surroundings or emitted by the object.

This is called the rendering equation. Materials which emit light have a positive , which in practice may be a constant or sampled from a texture. is more complex and depends on how all the lights of the scene interact with the material of the object at .

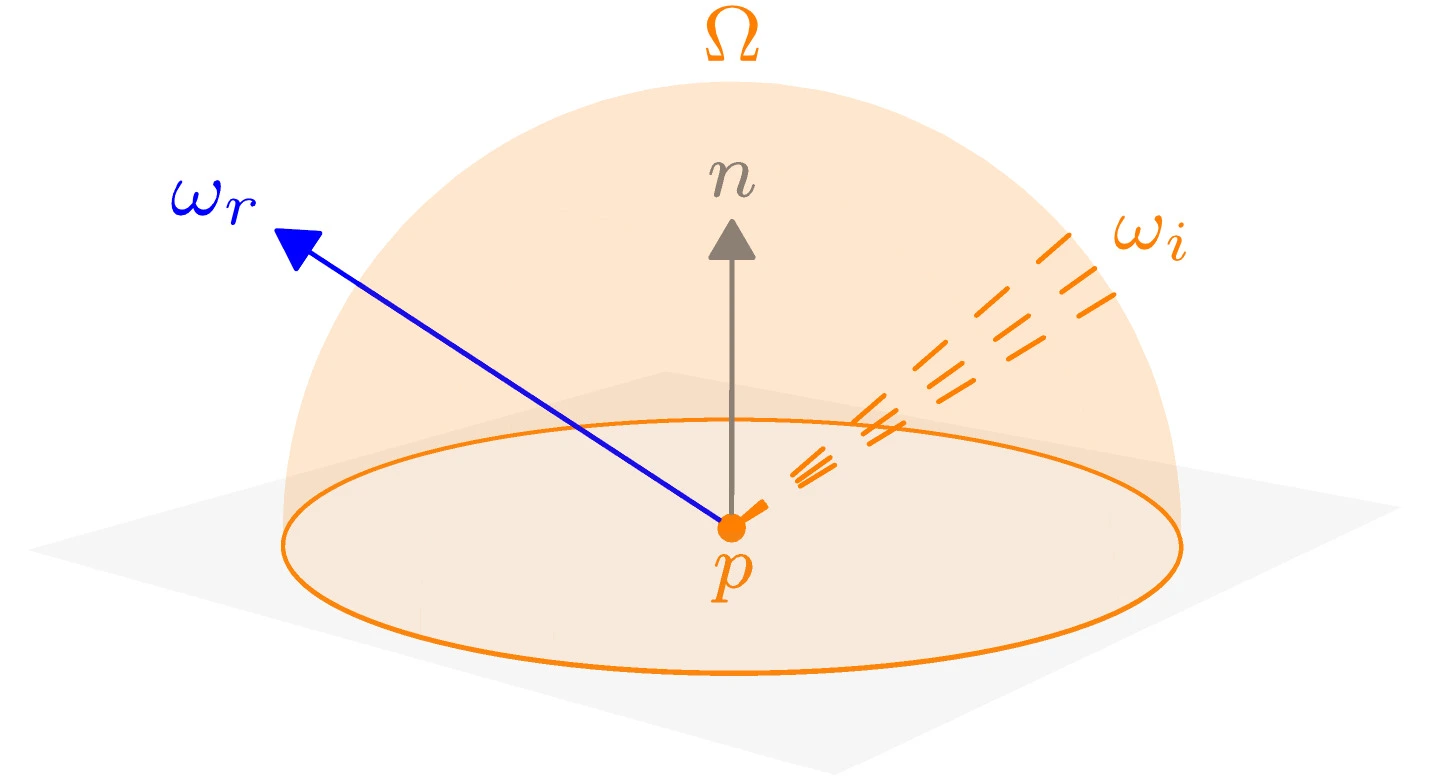
As mentioned earlier, the point is analogous to a small planar area with normal . Light which reflects off the surface can not come from behind the plane, so we consider only incident radiances directed from a hemisphere lying on the surface. This assumption precludes subsurface scattering effects (light hitting another point on the surface, scattering through the surface, and emerging inside ) which are significant in materials such as skin and water.

The hemisphere considers light from all directions incident on point .

We are trying to find the reflected radiance . This depends on all the light hitting which means we need to know the irradiance at . In the same manner we converted radiance to irradiance, we can convert incident radiances into an irradiance onto the surface. A function called the bidirectional reflectance distribution function (BRDF, units of ) then tells us what proportion of irradiance becomes radiance towards a view direction.

In this article, the notation will mean a solid angle which is directed towards .

You may be wondering why the BRDF is defined in terms of incident irradiance and not radiance, it is so that a BRDF does not vary systematically with light direction. This does not mean the BRDF does not depend on light direction, only that it's directionality is explained by the reflection of the material itself and not by the projection of flux. Another way of thinking about this is that the term projects the incident radiance onto the area . This theoretical understanding can be checked by substituting the definitions of irradiance, radiance and the BRDF (formalised below) noting that

BRDF

Slices from the BRDFs of different materials showing how reflection varies according to incident direction, from the MERL BRDF dataset.

BRDF is the proportion of radiance reflected towards for a certain irradiance from ,

Since the BRDF is defined by input irradiance, energy conservation can be guaranteed if the reflected radiances are together less than the incident irradiance. Using the same conversion from radiance to irradiance, this time for the reflected radiances, we can ensure energy conservation if

To satisfy the principle of Helmholtz reciprocity we should also be able to swap incident and reflected directions,

Different materials have different BRDFs which can be measured empirically or calculated from theoretical models. PBR consists of a group of energy conserving BRDFs which are usually derived from the microfacet model. Before deriving and explaining the microfacet BRDF we will derive some simpler BRDFs which will be important later.

Lambertian

The tiny facets of ice crystals in unpacked snow make it close to an ideal lambertian material. "Snowy Hillside, Creag a' Bhealaich, Sutherland" by Andrew Tryon, Creative Commons.

The simplest possible BRDF would be some constant, energy conserving value. This corresponds to a material which reflects light in every direction with equal radiance. A material may only be slightly lambertian, the part of the reflection which is lambertian is called the diffuse reflection.

When light hits a surface we usually think of it bouncing off like a mirror, how does a lambertian material fit into this model? While it's true that some light reflects off a surface like a mirror, this is the specular part of the reflection, some light is also transmitted into the material's surface. For most materials, transmitted light continues to be scattered in the subsurface of the material until it is directed back out, now in a random direction but still close to where it entered. This is diffuse reflection.

Yellow light hits a surface, the green wavelengths are absorbed in the subsurface and the red wavelengths scatter diffusely making the material appear red.

In coloured materials, some wavelengths of light are absorbed by the material in the process of refracting. These wavelengths are removed from the diffuse reflection, giving the material a colour. The diffuse reflection's colour from incident white light is called the albedo of a material.

Since the Lambertian BRDF is uniform we can set where is the albedo. Assuming a constant BRDF and ensuring energy conservation (derivation) we find

This is the Lambertian BRDF.

Mirror

Mirror ball ornament demonstrating specular reflection, CC0.

Metals, especially highly polished metals, reflect light to produce a mirrored appearance. For now we will consider the case of a perfect mirror which reflects all incident light specularly. Unlike diffuse reflection, specular reflection is usually considered to not have a colour because the light is not absorbed by refracting within the material.

BRDF of a perfect mirror for some specific incident direction.

The law of reflection tells us the reflected light is the incident light flipped about the normal. This means the mirror BRDF should only be positive when the reflection direction equals the incident direction flipped about the normal. The BRDF of a perfectly planar mirror can be expressed in two equivalent ways, in terms of the halfway vector , or polar and azimuthal angles.

where . is the Dirac delta function, which is positive only when . In this case means the delta function is positive only when the halfway vector aligns with the normal vector . The mirror BRDF is energy conserving (derivation).

Specular Microfacet

If you scratch a metal it becomes less shiny, and polishing makes it more shiny. In scratching the metal we are changing the microscopic surface of the metal to be more rough. A material's microsurface can be very complicated so we make an assumption that materials microsurfaces only vary in one parameter, roughness. We also assume that there are no overhangs in the microsurface.

Microsurface of gypsum, coloured SEM by Steve Gschmeissner.

The microfacet model accounts for roughness by treating our area as consisting of many smaller planes, called microfacets, which have different orientations. The normal of a microfacet is called a micronormal () as opposed to the macronormal (). Materials which are smoother have more micronormals which align with the macronormal and rougher materials have micronormals in more varied orientations.

Microsurface of a mirror, the roughness is as all micronormals align with the macronormal.

Microsurface of a rough material, light is reflected in many directions and some reflections are blocked.

If we consider microfacets of every possible orientation and add their contributions we can find the overall BRDF of the macrosurface,

where is a hemisphere. and are how visible the microfacet is along the incident and refracted directions respectively. This accounts for the difference in projected areas for microfacets of different orientations. This is separate to the geometry term which accounts for one facet blocking another facet.

Each microfacet has it's own BRDF , in this section we are going to assume mirror-like microfacets that only reflect specularly.

Roughness

Roughness is a measure of the microscopic bumpiness, a more rigorous definition is it is the variance in the orientations of the a material's microfacets. Assuming microfacets on average point towards the macronormal, then rougher materials have more micronormals pointing in different directions. The roughness is usually represented by which is between and . Disney suggested a more visually "linear" roughness parameter used when authoring which is common in roughness textures.

Microfacet BRDF

If each microfacet is assumed to be mirror-like and has perfect reflectance () then from the mirror BRDF derived earlier,

where is some function which ensures energy conservation. We need to solve for , our energy conservation integral requires

The delta function means that rather than having to sum over all incoming light, we only care about light coming from a direction our micronormal can reflect, when . For this reason, if the integral can be made in terms of instead of we can solve for . So we write

by change of variables.

We now need to find , that is how changes relative to . This can be solved geometrically by projecting the translated solid angle, the full derivation is long but interesting. We find

Substituting back into our energy conservation integral,

The delta function enforcing allowing us to eliminate the integral and yielding

Substituting , our microfacet BRDF is

The overall specular BRDF, made by summing the microfacets, is

Again, the delta function eliminates the integral and enforces . This make sense intuitively, since we only care about microfacets when they can actually reflect light, meaning their normals align with the halfway vector. Finally

Density Term

is the probability density for a micronormal directed into the solid angle from direction . If you think of each microfacet as occupying tiny areas , then if we project each microfacet flat, they should together cover our macro area . This can be expressed as the following condition on

A valid density term should both fit this condition and be physically plausible. Since there can't be overhangs, assume if not stated that each distribution is defined to equal when .

There are different models of rough surfaces, one idea is to consider the height at each point on the surface as following a gaussian distribution with variance set to the roughness parameter . This is called the Beckmann distribution, the height distribution is converted to a probability distribution over solid angles,

Another model is GGX or the Trowbridge-Reitz distribution proposed by Walter et al.. The GGX distribution better matches empirical measurements of rough material, which have longer tails of steeply angled microfacets than predicted by the Beckmann distribution. The probability distribution is

The GGX distribution is also simpler to calculate. The GGX distribution can be shown to fit our area rule as well:

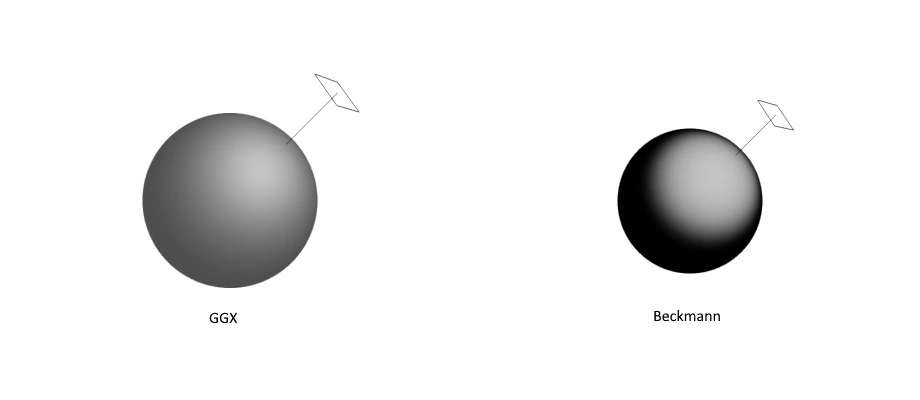
The distributions presented here assume a constant roughness across our macrofacet, this is not true for some materials. Materials such as brushed metal can have a different "roughness" for different viewing direction, meaning the microfacets are aligned differently along different directions in the material. This is called anisotropic reflection, as opposed to the isotropic reflection presented here.

Visualisation of the GGX and Beckmann density functions. For low roughness materials an off-peak bright spot is visible.

Geometry Term

The geometry term defines the proportion of the microfacet surface which is visible from both the incident and reflected directions. Light which would hit a microfacet may be blocked by another part of the surface, this is called shadowing. Alternatively, reflected light may be blocked from the viewer by the surface, called occlusion.

A rough surface which shows both shadowing and occlusion effects.

Since we don't know the actual microsurface, the geometry term tells us the expected degree of occlusion and shadowing for a microfacet distribution.

Smith suggested an approximation for the geometry term . Helmoholtz reciprocity requires that the amount a microfacet is expected to be visible is the same from both the incident and reflected directions. Let the expected amount that the microfacet is visible from be . Assuming that the visibility from and are independent then our overall geometry term is

This is an approximation because the visibility is not actually independent, for example a microfacet in a deep V is less visible from both directions. This is called an uncorrelated geometry function, as opposed to correlated.

Smith derived a method to calculate for any distribution of microfacets (from the density term ). This technique can be used to derive the Smith-GGX shadowing function, which was approximated by Schlick,

Alternatively Earl Hammon Jr also suggested a cheap approximation to a correlated geometry term based on ray traced results,

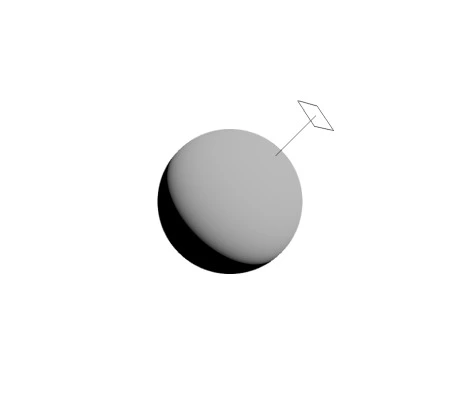
Visualisation of the geometry term, all those presented here look similar.

PBR

Fresnel Equation

In solving our specular microfacet BRDF we assumed that each microfacet was a perfect mirror, but as discussed when deriving the Lambertian BRDF, some of the light is not reflected, but rather scattered inside the material.

Some proportion of the incident energy is transimitted, and some is reflected.

The fresnel equations describe the proportion of incident radiance which is transmitted through a boundary, such as from air to our material. is a simplified form of the full Fresnel equation, defined as the proportion of unpolarized light which is specularly reflected from an air-dielectric boundary. depends on the incidence angle and the index of refraction (IOR) of the dielectric. The full Fresnel equation can be computationally expensive, Schlick's approximation

is commonly used instead, where is the colour of specularly reflected white light which was incident with the normal. The Schlick approximation is a Padé approximation (similar to a taylor series) using the conditions that the reflection should be when incident light is perpendicular and when incident light is tangent. The Schlick approximation has the advantage that the mediums' IORs don't have to be known, only which is easily measured. The derivation of the Schlick approximation is beyond this post but is well explained by the original paper.

A dialetric's is closer to white, meaning specular reflection is not tinted. A conductor's specular colour is closer to it's "albedo" or base colour, since the diffuse reflections disappear and the specular reflection must account for what colour the material has.

An sphere shaded by the Fresnel-Schlick approximation, grazing angles (light tangent to the surface) cause stronger specular reflections.

Specular and Diffuse

Our final PBR BRDF must combine the specular microfacet with a diffuse reflection. The specular reflection only occurs when light is not transmitted. Using the Fresnel equation where the boundary is oriented towards the microfacets we find that the specular reflection is

Light which is not specularly reflected should be diffusely reflected instead. This would require solving our microfacet BRDF again for the case of a Lambertian microfacet BRDF (). Unfortunately, our microfacet integral

has no closed form solution since there is no longer a delta function to eliminate the integral. It is simpler if we ignore the microfacets for the Lambertian and use the macrofacet normal instead.

Our final PBR microfacet BRDF is then

Using the rendering equation, the radiance directed towards the viewer is

This can be solved analytically using IBL or, assuming we only have analytically light sources (eg. directional lights) in our scene, for a set of analytical light sources

Code

The code for direct lighting of a dielectric material with PBR is found below for reference. There are some approximation used which can be found or derived from Edwards et al.. This code is for illustration purposes.

#define M_PI    3.14159265358979323846264338327950288
#define EPSILON 1.19209e-07

uniform float time;

uniform int G2_mode;
uniform int D_mode;
uniform float alpha;
uniform float dir_radiance;
uniform vec3 albedo;
uniform vec3 specular;
uniform vec3 emissive;

varying vec4 p;
varying vec3 n;

vec3 F_Schlick(float cLdotH, vec3 F0) {
  return F0 + (1.0-F0)*pow(1.0 - cLdotH, 5.0);
}

float G2_GGX_corr(float cLdotN, float cVdotN) {
  // Correlated Approximation
  float nom = cLdotN * cVdotN;
  float denom = mix(2.0*nom, cLdotN + cVdotN, alpha) + EPSILON;
  return nom / denom;
}

float G2_GGX_uncorr(float cLdotN, float cVdotN) {
  // Uncorrelated Approximation
  float nom = 4.0 * cLdotN * cVdotN;
  float denom = ((2.0 - alpha)*cLdotN + alpha) * ((2.0 - alpha)*cVdotN + alpha);
  return nom / denom;
}

float G1_Beckmann(float cXdotN) {
  float a = 1.0 / (alpha*sqrt(1.0 / (cXdotN*cXdotN + EPSILON) - 1.0) + EPSILON);
  float a2 = a*a;

  return (a < 1.6) ? ((3.535*a + 2.181*a2) / (1.0 + 2.276*a + 2.577*a2)) : 1.0;
}

float G2_Beckmann_uncorr(float cLdotN, float cVdotN) {
  return G1_Beckmann(cLdotN) * G1_Beckmann(cVdotN);
}

// Derived from Λ = (1 - G1) / G1
float A_Beckmann(float cXdotN) {
  float a = 1.0 / (alpha*sqrt(1.0 / (cXdotN*cXdotN + EPSILON) - 1.0) + EPSILON);
  float a2 = a*a;

  return (a < 1.6) ? ((1.0 - 1.259*a + 0.396*a2) / (3.535*a + 2.181*a2)) : 0.0;
}

// G2 = 1 / (1 + Λ(i) + Λ(r))
float G2_Beckmann_corr(float cLdotN, float cVdotN) {
  return 1.0 / (1.0 + A_Beckmann(cLdotN) + A_Beckmann(cVdotN));
}

float D_Beckmann(float HdotN) {
  float a2 = alpha*alpha;
  float c2 = HdotN*HdotN;

  float t2 = 1.0/(c2+EPSILON) - 1.0;
  float nom = exp(-t2/a2);
  float denom = M_PI*a2*c2*c2 + EPSILON;
  return nom / denom;
}

float D_GGX(float HdotN) {
  float a2 = alpha*alpha;
  float c2 = HdotN*HdotN;

  float nom = a2;
  float denom = M_PI*(c2 * (a2 - 1.0) + 1.0)*(c2 * (a2 - 1.0) + 1.0);
  return nom / denom;
}

vec3 L_r(vec3 N, vec3 V, float cVdotN, vec3 L, float radiance) {
    vec3 H = normalize(V + L);
    float cLdotN = max(dot(L,N),0.0);
    float cLdotH = max(dot(L,H),0.0);
    float HdotN = dot(H,N);

    vec3 F = F_Schlick(cLdotH, specular);
    float D = D_GGX(HdotN);
    float G2 = G2_GGX_corr(cLdotN, cVdotN);

    vec3 brdf_s = F*D*G2 / (4.0 * cLdotN * cVdotN + EPSILON);
    vec3 brdf_d = (1.0 - F) * albedo / M_PI;

    return (brdf_s + brdf_d)*radiance*cLdotN;
}