August, 2022
Adapting Spline Algorithms to Draw Proteins

Proteins are the building blocks of our cells and allow the incredible complexity of biology. Models of protein's structures that allow scientists to quickly compare and understand a protein's features are hence important. A common model of proteins are ribbon diagrams, which have been around since the 1980s. They were originally hand drawn but were quickly being created by computers. A ribbon diagram shows the shape of a protein by drawing 'ribbons' between the alpha-carbons of a protein. Alpha-carbons are the central atom in the peptide bond which joins the amino-acid's together in a polypeptide chain. A protein is a specific folding of this polypeptide chain. Looking at only the alpha-carbons simplifies the thousands of individual atoms down to relatively few points which can be connected into a recognisable shape.
Reading Protein Files
Before we can create our diagrams we first need the atoms and other information about the protein's structure. The Worldwide Protein Data Bank provides PDB files which contains scans of protein structures in a well documented file format. After loading the PDB we have the atoms and bond position, along with some extra structure information. In the online viewer demo, reading and reconstructing the structure is quick enough with WASM that this does not need to be cached, the PDB is re-processed every page load.
Rendering The Proteins
To render our proteins to the screen we need to form meshes which the GPU can efficiently draw. These meshes consist of triangles, each consisting of three vertices. The collection of triangles together enclose the ribbons which make up the diagram. To enable correct lighting we also need a normal for each vertex. Once you have a mesh you can draw the mesh with any 3D program you like or export a 3D model file.

The vertices, edges and triangles which enclose each ribbon. Each vertex needs a normal for correct shading. Where the structure is smooth, vertices and normals are shared, if instead we want sharp edges the triangle's vertices cannot be shared.
Creating The Ribbons
Creating a ribbon consists of two steps, fitting a spline to the alpha-carbons and extruding a 'profile' along this spline. A spline takes a pair of points and creates a curve which consists of many points which smoothly move between the pair. To extrude our spline we have to know the normal and tangent at each of these points. A profile is the shape of the ribbon's cross section at each point in the spline and can be circular, rectangular or some interpolated shape.
The Spline Algorithm
The spline algorithm was the main challenge here because conventional algorithms did not produce good results. Before creating the spline I first average adjacent alpha-carbon positions to create a smoother look, I then choose tangents for each point. You could use more chemically accurate tangents but I used a Cardinal interpolation to achieved a smoother look. The Cardinal method uses a dampened vector between adjacent position, so that the tangent is given by
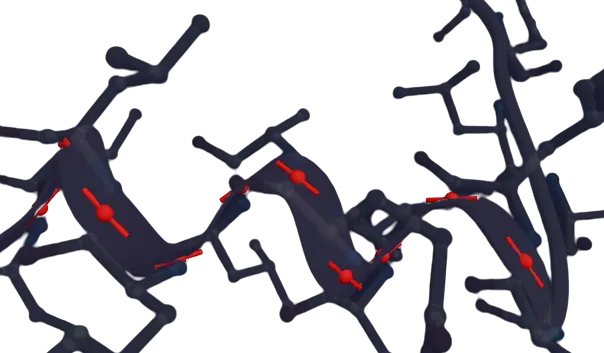
Averaged points and their tangents shown in red with parameter (
To actually generate the spline, it's important that the spline not only smoothly interpolates position but also tangent, normals and binormals. That is, the spline's first and second derivatives must be continuous. Specifying the tangents at each point ensures that adjacent splines have matching first derivatives but not second derivates. A quadratic spline would ensure smoothness, but sacrifices smoothness and I found that this produces a poor result. Rather, discarding the true normal and calculating the normal from the current tangent and previous point's normal is more effective. To increase smoothness, set the endpoint second derivative to zero, as in the natural Hermite Cubic. This ensures continuity, since the continuity of the tangents are guaranteed and simplifies calculation. If the previous normal is invalid I set the binormal to the perpendicular component, relative to the tangent, of the average of the endpoints' binormals, but this is a fairly arbitrary choice which I did not experiment with.
The position
And the tangent
The tangent is then be normalized and used to calculate the binormal and normal
In code this specific spline interpolation algorithm looks like the following,
Spline& Hermite(Frame start, Frame end, glm::vec3& prev_n, float t = 1.0) {
auto& p0 = start.position;
auto& p1 = end.position;
auto& m0 = start.tangent;
auto& m1 = end.tangent;
auto& n0 = start.normal;
auto& n1 = end.normal;
auto& b0 = start.binormal;
auto& b1 = end.binormal;
auto bref = (b0 + b1) / 2.f;
for (int i = 0; i < N; i++) {
auto t1 = ((float)i / (N - 1)) * t;
auto t2 = t1 * t1;
auto t3 = t1 * t2;
auto p = (2 * t3 - 3 * t2 + 1) * p0 + (t3 - 2 * t2 + t1) * m0 + (-2 * t3 + 3 * t2) * p1 + (t3 - t2) * m1;
auto tn = (6 * t2 - 6 * t1) * p0 + (3 * t2 - 4 * t1 + 1) * m0 + (-6 * t2 + 6 * t1) * p1 + (3 * t2 - 2 * t1) * m1;
tn = glm::normalize(tn);
glm::vec3 bn;
if (glm::length(prev_n) > 0.001) {
bn = glm::normalize(glm::cross(tn, prev_n));
} else {
bn = perpendicular_component(bref, tn);
}
auto n = glm::cross(bn, tn);
frames[i].position = p;
frames[i].tangent = tn;
frames[i].normal = n;
frames[i].binormal = bn;
prev_n = n;
}
return *this;
}